Naive Model Time Series
Bootstrapping time series data has special challenges. Simulate the model repeatedly, each time substituting resampled residuals for original residuals. 24 For example, let's fit the AR(1) data to a model. In fact, the naive bootstrap works poorly. 36 The maximum entropy bootstrap preserves the gross.
In other words, the naive forecast of 'next month's coil prices will be the same as this month's coil prices' is more accurate (at almost every forecast horizon) than 7 extremely sophisticated time series models. Associative and Time Series Forecasting Models. Associative and Time Series Forecasting involves using past data to generate a number, set of numbers, or scenario that corresponds to a future occurrence. It is absolutely essential to short-range and long-range planning. Simple uses of this model include “naive” forecasting.
I am working on a small project where we are trying to predict the prices of commodities (Oil, Aluminium, Tin, etc.) for the next 6 months. I have 12 such variables to predict and I have data from Apr, 2008 - May, 2013. How should I go about prediction? I have done the following:. Imported data as a Timeseries dataset. All variable's seasonality tends to vary with Trend, so I am going to multiplicative model. I took log of the variable to convert into additive model.
Naive Model Time Series 2016
For each variable decomposed the data using STL I am planning to use Holt Winters exponential smoothing, ARIMA and neural net to forecast. I split the data as training and testing (80, 20). Planning to choose the model with less MAE, MPE, MAPE and MASE.
Am I doing it right? Also one question I had was, before passing to ARIMA or neural net should I smooth the data?
If yes, using what? The data shows both Seasonality and trend. EDIT: Attaching the timeseries plot and data Year. The approach that you have taken is reasonable. If you are new to forecasting, then I would recommend following books:. by Makridakis, Wheelright and Hyndman.
by Hyndman and Athanasopoulos. The first book is a classic which I strongly recommend. The second book is an open source book which you can refer for forecasting methods and how it is applied using R open source software package. Both the books provide good background on the methods that I have used.
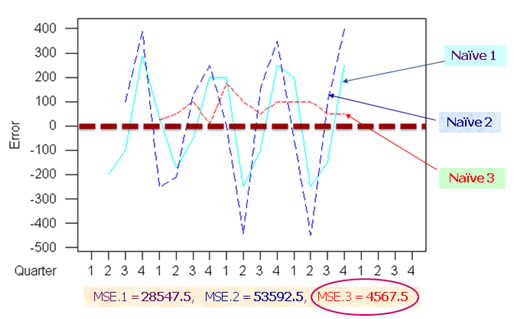
If you are serious about forecasting, then I would recommend by Armstrong which is collection of tremendous amount of research in forecasting that a practitioners might find it very helpful. Coming to your specific example on coil, it reminds me of a concept of which most textbooks often ignore. Some series such as your series simply cannot be forecasted because it is pattern less as it doesn't exhibit trend or seasonal patters or any systematic variation.
In that case I would categorize a series as less forecastable. Before venturing into extrapolation methods, I would look at the data and ask the question, is my series forecastable?In this specific example, a simple extrapolation such as forecast which uses the last value of the forecast has been found to be most accurate. Also one additional comment about neural network: Neural networks are notoriously know to fail in. I would try traditional statitical methods for time series before attempting to use neural networks for time series forecasting tasks. I attempted to model your data in R's forecast package, hopefully the comments are self explanatory.
Given the rise of smart electricity meters and the wide adoption of electricity generation technology like solar panels, there is a wealth of electricity usage data available. This data represents a multivariate time series of power-related variables that in turn could be used to model and even forecast future electricity consumption. In this tutorial, you will discover how to develop a test harness for the ‘household power consumption’ dataset and evaluate three naive forecast strategies that provide a baseline for more sophisticated algorithms. After completing this tutorial, you will know:. How to load, prepare, and downsample the household power consumption dataset ready for developing models. How to develop metrics, dataset split, and walk-forward validation elements for a robust test harness for evaluating forecasting models.
How to develop and evaluate and compare the performance a suite of naive persistence forecasting methods. Let’s get started. How to Develop and Evaluate Naive Forecast Methods for Forecasting Household Electricity Consumption Photo by Philippe Put, some rights reserved. Tutorial Overview This tutorial is divided into four parts; they are:. Problem Description.
Load and Prepare Dataset. Model Evaluation. Naive Forecast Models Problem Description The ‘Household Power Consumption‘ dataset is a multivariate time series dataset that describes the electricity consumption for a single household over four years. The data was collected between December 2006 and November 2010 and observations of power consumption within the household were collected every minute.
Time Series Model Example
It is a multivariate series comprised of seven variables (besides the date and time); they are:. globalactivepower: The total active power consumed by the household (kilowatts).
globalreactivepower: The total reactive power consumed by the household (kilowatts). voltage: Average voltage (volts). globalintensity: Average current intensity (amps). submetering1: Active energy for kitchen (watt-hours of active energy). submetering2: Active energy for laundry (watt-hours of active energy). submetering3: Active energy for climate control systems (watt-hours of active energy).
Active and reactive energy refer to the technical details of alternative current. A fourth sub-metering variable can be created by subtracting the sum of three defined sub-metering variables from the total active energy as follows. Submeteringremainder = (globalactivepower. 1000 / 60) – (submetering1 + submetering2 + submetering3) Load and Prepare Dataset The dataset can be downloaded from the UCI Machine Learning repository as a single 20 megabyte.zip file:.
Radiator RADIUS server is flexible, extensible, and authenticates from a huge range of auth methods, including Wireless, TLS, TTLS, PEAP, LEAP, FAST, SQL. “I purchased a radiator from Mac’s about two weeks ago and would like you to know that Brad did a great job in helping me fit the radiator to my 1938 Pontiac. Find great deals on eBay for mac radiator. Shop with confidence. Mac Radiators was born 4 years ago from Mac's desire to address that part of the racing radiators market that was neglected by the big companies, the track day enthusiast, weekend racer and small teams that cant waste 550-650 on a racing radiator. Radiator for mac.
householdpowerconsumption.zip Download the dataset and unzip it into your current working directory. You will now have the file “ householdpowerconsumption.txt” that is about 127 megabytes in size and contains all of the observations. We can use the readcsv function to load the data and combine the first two columns into a single date-time column that we can use as an index.
Tocsv ( ‘householdpowerconsumption.csv’ ) Running the example creates the new file ‘ householdpowerconsumption.csv‘ that we can use as the starting point for our modeling project. Model Evaluation In this section, we will consider how we can develop and evaluate predictive models for the household power dataset.
This section is divided into four parts; they are:. Problem Framing. Evaluation Metric. Train and Test Sets. Walk-Forward Validation Problem Framing There are many ways to harness and explore the household power consumption dataset.

Naive Model Time Series List
In this tutorial, we will use the data to explore a very specific question; that is: Given recent power consumption, what is the expected power consumption for the week ahead? This requires that a predictive model forecast the total active power for each day over the next seven days. Technically, this framing of the problem is referred to as a multi-step time series forecasting problem, given the multiple forecast steps. A model that makes use of multiple input variables may be referred to as a multivariate multi-step time series forecasting model.
A model of this type could be helpful within the household in planning expenditures. It could also be helpful on the supply side for planning electricity demand for a specific household.
This framing of the dataset also suggests that it would be useful to downsample the per-minute observations of power consumption to daily totals. This is not required, but makes sense, given that we are interested in total power per day. We can achieve this easily using the resample function on the pandas DataFrame. Calling this function with the argument ‘ D‘ allows the loaded data indexed by date-time to be grouped by day (see all offset aliases). We can then calculate the sum of all observations for each day and create a new dataset of daily power consumption data for each of the eight variables.
The complete example is listed below. Tocsv ( ‘householdpowerconsumptiondays.csv’ ) Running the example creates a new daily total power consumption dataset and saves the result into a separate file named ‘ householdpowerconsumptiondays.csv‘. We can use this as the dataset for fitting and evaluating predictive models for the chosen framing of the problem. Evaluation Metric A forecast will be comprised of seven values, one for each day of the week ahead. It is common with multi-step forecasting problems to evaluate each forecasted time step separately. This is helpful for a few reasons:.
To comment on the skill at a specific lead time (e.g. +1 day vs +3 days). To contrast models based on their skills at different lead times (e.g. Models good at +1 day vs models good at days +5). The units of the total power are kilowatts and it would be useful to have an error metric that was also in the same units.
Both Root Mean Squared Error (RMSE) and Mean Absolute Error (MAE) fit this bill, although RMSE is more commonly used and will be adopted in this tutorial. Unlike MAE, RMSE is more punishing of forecast errors. The performance metric for this problem will be the RMSE for each lead time from day 1 to day 7. As a short-cut, it may be useful to summarize the performance of a model using a single score in order to aide in model selection. One possible score that could be used would be the RMSE across all forecast days.
The function evaluateforecasts below will implement this behavior and return the performance of a model based on multiple seven-day forecasts. Return score, scores Running the function will first return the overall RMSE regardless of day, then an array of RMSE scores for each day.
Train and Test Sets We will use the first three years of data for training predictive models and the final year for evaluating models. The data in a given dataset will be divided into standard weeks.
These are weeks that begin on a Sunday and end on a Saturday. This is a realistic and useful way for using the chosen framing of the model, where the power consumption for the week ahead can be predicted. It is also helpful with modeling, where models can be used to predict a specific day (e.g. Wednesday) or the entire sequence. We will split the data into standard weeks, working backwards from the test dataset.
The final year of the data is in 2010 and the first Sunday for 2010 was January 3rd. The data ends in mid November 2010 and the closest final Saturday in the data is November 20th. This gives 46 weeks of test data.
The first and last rows of daily data for the test dataset are provided below for confirmation. 209.04 Walk-Forward Validation Models will be evaluated using a scheme called walk-forward validation. This is where a model is required to make a one week prediction, then the actual data for that week is made available to the model so that it can be used as the basis for making a prediction on the subsequent week.
This is both realistic for how the model may be used in practice and beneficial to the models allowing them to make use of the best available data. We can demonstrate this below with separation of input data and output/predicted data. Print ( ‘%s: %.3f%s’% ( name, score, sscores ) ) We now have all of the elements to begin evaluating predictive models on the dataset. Naive Forecast Models It is important to test naive forecast models on any new prediction problem. The results from naive models provide a quantitative idea of how difficult the forecast problem is and provide a baseline performance by which more sophisticated forecast methods can be evaluated. In this section, we will develop and compare three naive forecast methods for the household power prediction problem; they are:. Daily Persistence Forecast.
Weekly Persistent Forecast. Weekly One-Year-Ago Persistent Forecast. Daily Persistence Forecast The first naive forecast that we will develop is a daily persistence model. This model takes the active power from the last day prior to the forecast period (e.g. Saturday) and uses it as the value of the power for each day in the forecast period (Sunday to Saturday). The dailypersistence function below implements the daily persistence forecast strategy. Show ( ) Running the example first prints the total and daily scores for each model.
We can see that the weekly strategy performs better than the daily strategy and that the week one year ago ( week-oya) performs slightly better again. We can see this in both the overall RMSE scores for each model and in the daily scores for each forecast day. One exception is the forecast error for the first day (Sunday) where it appears that the daily persistence model performs better than the two weekly strategies.
We can use the week-oya strategy with an overall RMSE of 465.294 kilowatts as the baseline in performance for more sophisticated models to be considered skillful on this specific framing of the problem. Week-oya: 465.294 550.0, 446.7, 398.6, 487.0, 459.3, 313.5, 555.1 A line plot of the daily forecast error is also created. We can see the same observed pattern of the weekly strategies performing better than the daily strategy in general, except in the case of the first day.
It is surprising (to me) that the week one-year-ago performs better than using the prior week. I would have expected that the power consumption from last week to be more relevant. Reviewing all strategies on the same plot suggests possible combinations of the strategies that may result in even better performance.